Orbital Computational Dynamics
Homework Help & Tutoring
We offer an array of different online Orbital Computational Dynamics tutors, all of whom are advanced in their fields and highly qualified to instruct you.
Orbital Computational Dynamics
Kepler's 3 Laws Governing Orbits
Orbital computational dynamics concerns the calculation of orbits, i.e. the circulation of a large object around a point. The complexity of a system can make it too complex to solve all equations by analytical approach, so numerical methods implemented on modern computers may be required. There are several techniques in use.
As an introduction to the subject, this article is going to present arguably the oldest application of orbital mechanics; Kepler's laws governing the motion of planets. They were presented as early as 1609 [1] and 1618 [2] by German Mathematician and Astronomer Johannes Kepler, working out of his observatory in the Prague [3]. They were based on huge amounts of data from the observations carried out in collaboration with Danish astronomer Tycho Brahe [4].This challenged contemporary scientific consensus of the old Copernicus model of celestial objects moving in circles around the Sun, also called the heliocentric planetary model [5] .
The laws are formulated as follows:
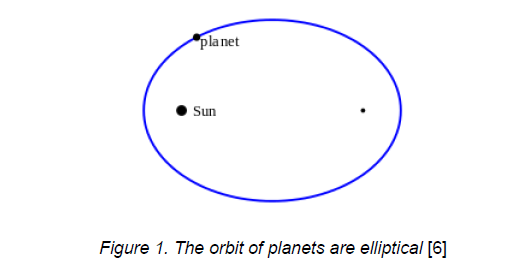
The motion of the planets is an elliptical orbit with the Sun as one the focal points (See Figure 1).
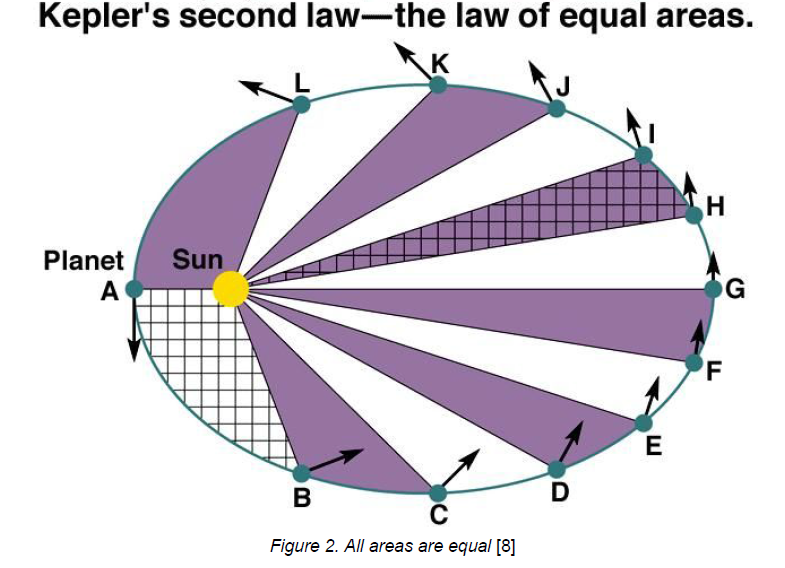
Remarkably, the second focal point depicted in Figure 1 is not a body of any kind, just an empty point in space. The most influential consequence of the First law is that the distance between the Sun and the planets vary [7]. The vector between any planet and the Sun sweeps out equal areas in any intervals of equal time (Figure 2).
For this to hold, the planets must move faster when they are closer to the Sun compared to when they are at a longer distance [9] . It also means that the Winter half of the year from Winter solstice to Summer solstice is slightly shorter than the Summer half by approximately 3 days [10]. Naturally, the opposite holds for the Southern Hemisphere.
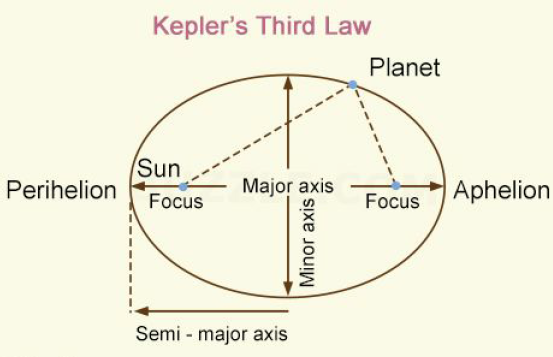
The square of the orbital period of a planet is proportional to the cube of the semimajor axes of its orbit [11]
A definition of the semimajor axis term can be seen in Figure 3.
The third law controls the length of the year for each of the planets in the solar system. The formula also includes mass and the Gravitational constant. There are quite a few interactive calculators available through the WWW, for example [13] Kepler’s laws were later confirmed and explained by more general laws of gravitation exposed by Isaac Newton.
References
1. Kepler, J: Astronomia nova. Prague 1609
2. Kepler, J: Harmonice Mundi . Prague 1618
3. Johannes Kepler. https://en.wikipedia.org/wiki/Johannes_Kepler Wikipedia
4. Supernovas: Making Astronomical History. Tycho and Kepler
5. Williams, M.: What is the HelioCentric Model of the Universe? Universe Today, 2016, http://www.universetoday.com/33113/heliocentricmodel/
6. Kepler’s Law of Planetary Motion https://en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion
7. Dictionary: Johannes Kepler: The Laws of Planetary Motion. The Spaceguard Foundation and of the Spaceguard System, http://spaceguard.rm.iasf.cnr.it/NScience/neo/dictionary/kepler.htm
8. Fix, John D.: Astronomy: Journey to the Cosmic Frontier. McGrawHill, 1999
9. Kepler’s 2nd Law: The Speeds of Planets . Windows to the Universe, National Earth Science Teachers Association, http://www.windows2universe.org/the_universe/uts/kepler2.html
10. Stern, David P.: More on Kepler’s Second Law: The Ratio of Velocities at Perigee and Apogee. From Stargazes to Starships, http://www.phy6.org/stargaze/Skepl2A.htm
11. Kepler’s Third Law. Boundless Textbooks. https://www.boundless.com/physics/textbooks/boundlessphysicstextbook/uniformcircularmotionandgravitation5/keplerslaws56/keplersthirdlaw26711197/
12. Johannes Kepler’s 3 Laws of Planetary Motion. Buzzle.com, http://www.buzzle.com/articles/johanneskeplers3lawsofplanetarymotion.html
13. Kepler’s 3rd Law Ultra Calculator. Software Systems, http://www.1728.org/kepler3a.htm
14. Newton, I.: Philosophiæ Naturalis Principa Mathematica. 1687
To fulfill our tutoring mission of online education, our college homework help and online tutoring centers are standing by 24/7, ready to assist college students who need homework help with all aspects of orbital computational dynamics. Our physics tutors can help with all your projects, large or small, and we challenge you to find better online orbital computational dynamics tutoring anywhere.
College Orbital Computational Dynamics Homework Help
Since we have tutors in all Orbital Computational Dynamics related topics, we can provide a range of different services. Our online Orbital Computational Dynamics tutors will:
- Provide specific insight for homework assignments.
- Review broad conceptual ideas and chapters.
- Simplify complex topics into digestible pieces of information.
- Answer any Orbital Computational Dynamics related questions.
- Tailor instruction to fit your style of learning.
With these capabilities, our college Orbital Computational Dynamics tutors will give you the tools you need to gain a comprehensive knowledge of Orbital Computational Dynamics you can use in future courses.
24HourAnswers Online Orbital Computational Dynamics Tutors
Our tutors are just as dedicated to your success in class as you are, so they are available around the clock to assist you with questions, homework, exam preparation and any Orbital Computational Dynamics related assignments you need extra help completing.
In addition to gaining access to highly qualified tutors, you'll also strengthen your confidence level in the classroom when you work with us. This newfound confidence will allow you to apply your Orbital Computational Dynamics knowledge in future courses and keep your education progressing smoothly.
Because our college Orbital Computational Dynamics tutors are fully remote, seeking their help is easy. Rather than spend valuable time trying to find a local Orbital Computational Dynamics tutor you can trust, just call on our tutors whenever you need them without any conflicting schedules getting in the way.