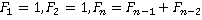Number Theory
Homework Help & Tutoring
We offer an array of different online Number Theory tutors, all of whom are advanced in their fields and highly qualified to instruct you.
Number Theory
The Fibonacci Numbers
Number theory deals with the analysis of integers, i.e. whole numbers without fractions or decimals. Many applications of modeling are by nature only valid for whole numbers and can never be parts of a number. For example, when counting people, or animals. They are ordered on the numbering line ranging from negative infinity, ... -3, -2, -1, 0, 1, 2, … up to positive infinity.
One important application of number theory is in the Fibonacci Numbers, presented originally in the 13th century in Liber Abaci [1]. This is widely regarded as a catalyst in bringing a more modern understanding of numbers, introducing the Arabic numbering system to Europe [2]. The system was formulated by Italian mathematics professor Leonardo Pisano Fibonacci, a mathematician from the Italian city of Pisa and widely renowned as one of the greatest mathematicians of the Medieval era [3] [4].
Fibonacci studied rabbit populations and looked at a simplified model of the reproduction formulated as: [5]
- Rabbits grow and can produce offspring after one month;
- Each female produces two new offspring (one male, one female) each month;
- No rabbits ever die.
This lead to the world famous equation: [6]
This may seem rather moderate at first sight, but leads to very high numbers as the index n grows:
|
n |
Fn |
|
10 |
55 |
|
30 |
832040 |
|
50 |
12586269025 |
|
100 |
354224848179261915075 |
|
300 |
222232244629420445529739893461909967206666939096499764990979600 |
Table 1. Some Fibonacci Numbers [7]
Although the Fibonacci numbers were formulated on a very idealized and simple model, they have relevance in many forms of combinatorics problems including stock trading, art, computer science and biology.
References
1. Fibonacci, L.P.: Liber Abaci. 1202.
2. The Life and Numbers of Fibonacci. Plus Maths, https://plus.maths.org/content/life-and-numbersfibonacci
3. Who was Fibonacci? Ron Knott, Surrey University, UK. http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibBio.html
4. Devlin, K.: The Man of Numbers, Fibonaccis Arithmetic Revolution, Walker and Company 2011.
5. Fibonacci and the rabbits the story. The Fibonacci Project, University of Bayreuth, Germany, http://fibonacci.uni-de/project/fibonacci-and-the-rabbits/the-story.html
6. Fibonacci Number, Wolfram Mathworld, http://mathworld.wolfram.com/FibonacciNumber.html
7. The First 2000 Fibonacci Numbers. The Online Encyclopedia of Integer Sequences, https://oeis.org/A000045/b000045.txt
To fulfill our tutoring mission of online education, our college homework help and online tutoring centers are standing by 24/7, ready to assist college students who need homework help with all aspects of number theory. Our mathematics tutors can help with all your projects, large or small, and we challenge you to find better online number theory tutoring anywhere.
College Number Theory Homework Help
Since we have tutors in all Number Theory related topics, we can provide a range of different services. Our online Number Theory tutors will:
- Provide specific insight for homework assignments.
- Review broad conceptual ideas and chapters.
- Simplify complex topics into digestible pieces of information.
- Answer any Number Theory related questions.
- Tailor instruction to fit your style of learning.
With these capabilities, our college Number Theory tutors will give you the tools you need to gain a comprehensive knowledge of Number Theory you can use in future courses.
24HourAnswers Online Number Theory Tutors
Our tutors are just as dedicated to your success in class as you are, so they are available around the clock to assist you with questions, homework, exam preparation and any Number Theory related assignments you need extra help completing.
In addition to gaining access to highly qualified tutors, you'll also strengthen your confidence level in the classroom when you work with us. This newfound confidence will allow you to apply your Number Theory knowledge in future courses and keep your education progressing smoothly.
Because our college Number Theory tutors are fully remote, seeking their help is easy. Rather than spend valuable time trying to find a local Number Theory tutor you can trust, just call on our tutors whenever you need them without any conflicting schedules getting in the way.